Introduction
In our previous post about quantum computing, Hadamard and Friends, we touched upon the Pauli group, a group of matrices over the complex domain that represents a collection of elementary quantum gates.
The wikipedia page on the Pauli group states that the group is isomorphic to the central product of the cyclic group of order four and the dihedral group of a square. In this post, we will create representations of various of these groups in Java and demonstrate the isomorphism for \(G_1\), the Pauli group on a single qubit.
Generating the Pauli Group
The Pauli group can be defined using three matrices over the complex domain: $$X=\begin{bmatrix}0&1\\1&0\end{bmatrix},\,Y=\begin{bmatrix}0&-i\\i&0\end{bmatrix},\,Z=\begin{bmatrix}1&0\\0&-1\end{bmatrix}.$$ Before you continue, note that the wikipedia page on Pauli matrices describes a lot of properties and applications of these matrices.
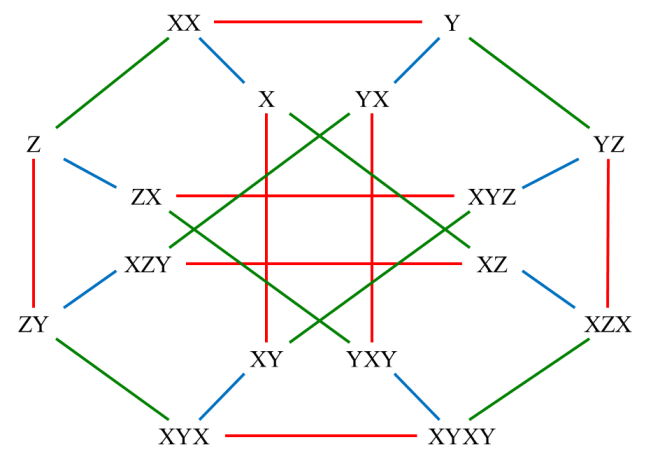
Generating the group using these generators, as illustrated in Generation of a Group, gives us a total of 16 elements: $$\begin{align}G_1=\{\,&X,\,Y,\,Z,\,XX,\,XY,\,XZ,\,YX,\,YZ,\,ZX,\,ZY,\\&XYX,\,XYZ,\,XZX,\,XZY,\,YXY,\,XYXY\,\}.\end{align}$$ The generation of the group can be illustrated using a Cayley graph:
Here, multiplication with \(X\), \(Y\) and \(Z\) are represented by a blue, red and green line respectively.
Note that all three generators \(X\), \(Y\) and \(Z\) are their own inverse. For example $$YY=\begin{bmatrix}0&-i\\i&0\end{bmatrix}\begin{bmatrix}0&-i\\i&0\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}=I.$$ This implies that all operations in the Cayley graph are symmetrical. We therefore use no arrows in the Cayley graph, and any edge can be used in both directions. As another consequence, the neutral element \(I\) is represented as \(XX\).
Each element of the group can be represented in many different ways. For example, it is easy to observe the following equations in the Cayley graph: $$XYZ=YZX=ZXY.$$ The generation process implicitly checks for equal matrices. The notation of the elements above is merely depending on the order in which the generators are combined. The first time a new matrix is obtained, it is added to the set, while subsequent occurrences of the same matrix will not be added to the set.
Enumerating the Pauli Group
The Pauli group can also be defined by enumeration of all elements, using the identity matrix and the generator matrices introduced earlier, multiplied by one of a number of complex factors: $$G_1=\{fA,f\in\{\pm 1,\pm i\},A\in\{I,X,Y,Z\}\}.$$ Consider the matrix multiplication $$XY=\begin{bmatrix}0&1\\1&0\end{bmatrix}\begin{bmatrix}0&-i\\i&0\end{bmatrix}=\begin{bmatrix}i&0\\0&-i\end{bmatrix}=iZ.$$ It is easy to verify that each element of the generated definiton of the group can be written as an element of the enumerated definition of the group. As such, the enumerated group is identical to the generated group. We intentionally do not use the term isomorphic, as the matrices in both groups are identical and the difference is merely in naming.
We can therefore rename the nodes in the Cayley graph based on this enumeration:
Alternative Generators
Using the Cayley graph, one can observe the symmetry of the generators, in the sense that an even permutation of the generators will not change the structure of the Cayley graph. An even permutation of \(X\), \(Y\) and \(Z\) still yields a correct Cayley graph, where the edges duly represent matrix multiplications. Odd permutations however would require some nodes to trade places in order for the group to be correctly represented.
Looking at the way the group is generated by the three generators, each combination of two generators will generate exactly half of the group. In fact, that is the case for any pair of independent elements of the group.
Applying the generators one after the other, alternatingly, enumerates half of the group in a loop. The third generator is required to get to the other half of the group, where the same loop structure occurs. In fact, that is the case for any combination of generators of the group.
We will now move on to an alternative construction of the Pauli group, as the central product of the cyclic group of order four and the dihedral group of a square.
The Cyclic Group of Order Four
The cyclic group of order 4 is a group with one generator that yields the identity after 4 applications. It can be defined as the additive group of integers modulo 4: $$C_4=\mathbb{Z}/4\mathbb{Z}=\{0,1,2,3\}.$$ Note that a number refers to the equivalence class of that number in the quotient group here.
As we can only represent finite groups, we cannot use the definition based on a quotient group of \(\mathbb{Z}\). We will be using the finite set of integers modulo 4 and define the addition operation on that set, as illustrated in Cyclic Groups.
The Cayley graph for the group is
In what follows, we will need the center of \(C_4\). The center of a group is defined as the set of elements that commute with every element in the group. The center of a group \(G\) is denoted and defined by $$Z(G)=\{z\in G|\forall g\in G, zg=gz\}.$$ As \(C_4\) is an Abelian group, its center is the group itself: $$Z(C_4)=C_4=\{0,1,2,3\}.$$ Note that we could just as well create a cyclic group of order 4 using for example the matrix representation of a 90 degrees rotation as a generator. Borrowing on the notation of the Pauli matrices, that would be using the matrix $$R=XZ=\begin{bmatrix}0&1\\1&0\end{bmatrix}\begin{bmatrix}1&0\\0&-1\end{bmatrix}=\begin{bmatrix}0&-1\\1&0\end{bmatrix}.$$ The group would then be defined as the set $$C_4=\{I,R,R^2,R^3\},$$ with composition (matrix multiplication) as an operation.
Note that we could have used any combination of two generators of the Pauli group, in any order, as they will all cycle after four applications. Defining \(R\) as \(XZ\) is just an example with an intuitive meaning.
We could use the matrix representation of \(C_4\) to continue. However, we opted for the integers modulo 4, just to illustrate using groups with different types of elements in our constructions.
The Dihedral Group of a Square
A dihedral group is the symmetry group of a regular polygon. In this case, we need the dihedral group of a square, denoted \(D_8\) in abstract algebra, denoted \(D_4\) in geometry. The group can be generated using two generators: a rotation over 90 degrees, denoted R, and mirroring against the verical axis, denoted M.
We can represent those generators by matrices once more, as transformations in a plane: $$M=\begin{bmatrix}1&0\\0&-1\end{bmatrix},\,R=\begin{bmatrix}0&-1\\1&0\end{bmatrix}.$$ Generating the group using these generators, as illustrated in Generation of a Group, gives us a set of 8 elements: $$D_8=\{I,R,RR,RRR,M,RM,RRM,MR\}.$$ with composition (matrix multiplication) as an operation.
The Cayley graph for this group is
A red arrow represents multiplication by \(R\), a blue line represents multiplication by \(M\). As before, as \(M\) represents a symmetric operation, the arrows for that generator have been left out.
In what follows, we will need \(Z(D_8)\), the center of \(D_8\). As illustrated in The Center of a Group, we get $$Z(D_8)=\{I,RR\}.$$ That is, besides the identity, \(RR\) is the only element that commutes with every other element in the group.
Note that our center is isomorphic to the cyclic group of order 2: $$Z(D_8)\cong C_2.$$
The Central Product
On the Wikipedia page on the Pauli group, we read that the Pauli group is isomorphic to the central product of the cyclic group of order four and the dihedral group of a square: $$G_1\cong C_4\circ D_8.$$ As a reminder, the Wikipedia page on the central product states that the central product is similar to the direct product, but in the central product two isomorphic central subgroups of the smaller groups are merged into a single central subgroup of the product.
The Direct Product
The set of elements of the direct product of \(C_4\) and \(D_8\) is the cartesian product of the factor groups: $$C_4\times D_8 = \{(n, A)\,|\,n\in C_4, A\in D_8\}.$$ The operation for the direct product is the pairwise application of the operations of the factor groups. Assuming that \(+\) is the group operation of \(C_4\), being the additive group of integers modulo 4, matrix multiplication in \(D_8\) is denoted by juxtaposition, and \(\times\) is the group operation of the direct product, we get: $$(n, A)\times (m, B) = (n+m, AB).$$
The Common Center
Looking at the centers of \(C_4\) and \(D_8\), it is easy to see that the maximum subgroup they have in common is isomorphic to \(C_2\), the cyclic group of order 2. Formulated over the respective alphabets, we get $$\{0, 2\}\cong\{I, RR\}\cong C_2.$$ We will therefore express the commonality using the subgroup \(Z\) of the direct product isomorphic to the common center of the factor groups as: $$Z=\{(0, I), (2, RR)\}\cong C_2.$$ Clearly, \((0, I)\) is the neutral element of the direct product, and consequently also of \(Z\). We quickly verify the cyclic nature of \(Z\), for illustration: $$(2, RR)\times (2, RR) = (2+2, RRRR) = (0, I).$$
An Alternative Definition of the Pauli Group
Now, finally, we are ready to try constructing our alternative Pauli group, as a quotient group we will refer to as \(F_1\), dividing the direct product by the subgroup \(Z\): $$G_1\cong F_1=(C_4\times D_8)/Z.$$ Although we did use the notion of a quotient group already talking about the set of integers modulo 4, we quickly repeat the definiton of a quotient group as given on Wikipedia: $$G/N=\{gN\,|\,g\in G\},$$ where \(G\) is a group and \(N\) is a normal subgroup. Here, \(gN\) is referred to as a coset of \(N\) in \(G\). Typically, different elements \(g\) will result in the same coset when applied to \(N\).
However, for simplicity in notation, for the representation of the quotient group, we will use a representative of each coset rather than the coset iself. For example, we will use \((1, M)\) as the representative of its coset $$(1, M)\times Z=\{(1, M), (3, RRM)\}$$ As such, and as illustrated in The Central Product, we get the following enumeration for the quotient group: $$\begin{align}F_1=\{&(0,I), (0,R), (0,M), (0,RR), (0,RM), (0,MR), (0,RRR), (0,RRM),\\&(1,I), (1,R), (1,M), (1,RR), (1,RM), (1,MR), (1,RRR), (1,RRM)\}\end{align}$$ So far so good, but is this group \(F_1\) really isomorphic to the Pauli group ?
Finding the Isomorphism
To verify whether \(F_1\) is isomorphic to \(G_1\), we have to find a bijection \(\phi\) between the elements of both groups that preserves the group operation. That is, for \(A\) and \(B\) elements of \(G_1\): $$\phi(AB)=\phi(A)\times\phi(B).$$ First of all, the number of elements is fine: \(F_1\) has 16 elements, just as the Pauli group. However, the remainder of the exercise is a bit harder.
We can restrict ourselves to defining the bijection for the generators only, and then verifying preservation of the operation on all combinations (including repetitions) of the generators.
Candidate mappings for the generators should respect a number of constraints. First of all, the identity element can be excluded. Secondly, all generators should be their own inverse, as is the case for \(X\), \(Y\) and \(Z\). This reduces the candidate set to seven elements: $$\{(0,M), (0,RR), (0,RM), (0,MR), (0,RRM), (1,R), (1,RRR)\}$$ Furthermore, logic dictates that in our combination of three generators, all basic building blocks should be represented, in particular the elements \(0\), \(1\), \(R\) and \(M\) of the respective factor groups. This leaves \(2\times 4\times 5=40\) possible combinations of three, ignoring order.
In the java section on Finding an Isomorphism, we do an exhaustive scan, mapping \(X\), \(Y\) and \(Z\) onto different combinations of elements of \(F_1\). Here, we limit ourselves to presenting one of the resulting isomorphisms: $$\phi(X)=(0, M),\,\phi(Y)=(0, RM),\,\phi(Z)=(1, R).$$ Once we have the bijection defined for the generators, the entire group structure follows nicely. This is illustrated once again by a Cayley diagram, the equivalent of the ones presented earlier, but now over our new alphabet:
Note that many more mappings are possible to define the isomorphism, given the symmetries of the Pauli group, and the one presented here represents just one possiblity.
Conclusions
We verified exhaustively that the Pauli group on a single qubit, typically defined as the group generated by three 2x2 matrices over the complex domain, is isomorphic to the central product of the cyclic group of order four and the dihedral group of a square. There's no magic involved here.
Java Implementation
However, the fun in this post is found in the way finite groups can be represented in Java, using whatever type of element and operation that suits the purpose. In addition, constructs such as the direct product, the center and the quotient of groups can be implemented generically on these groups. In what follows, we will illustrate this implementation in Java.
Group Representation
We start our implementation in Java with the definition of the interface that defines a group:
public interface Group<T> {
public Set<T> getElements();
public T getIdentity();
public T multiply(T a, T b);
}
It is defined as a generic interface, where the element type is a parameter. We do not impose any explicit type for the elements of a group, merely that the element type implements
equals and hashcode.
A group should be able to produce its elements, as a Java
Set, it provides access to the neutral element, and it implements the group operation, referred to as mul.
Note that the group operation could be implemented on the element as well, but that would require an explicit element type, which strongly reduces the genericity of the group implementation.
Also note that we did not include the concepts of symmetric elements, as we do not need them in the scope of this post. We are confident that this could be added to the implementation without breaking the approach taken.
Enumeration of a Group
As a first implementation of the group interface we will focus on an enumerated group:
public class EnumeratedGroup<T> implements Group<T> {
private Set<T> elements;
private T identity;
private BiFunction<T, T, T> operation;
public EnumeratedGroup(Set<T> elements, T identity, BiFunction<T, T, T> operation) {
this.elements = new HashSet<>(elements);
this.identity = identity;
this.operation = operation;
}
...
@Override
public T multiply(T a, T b) {
return operation.apply(a, b);
}
}
The constructor of the group requires the set of elements of the group, an explicit reference to the identity element, and a binary function that implements the group operation.
The implementation of this class is straightforward now. You will want to add getters and at least provide an implementation for
toString.
We only included the implementation of the multiply function, just in case.
Generation of a Group
Next comes the implementation of a group specified using a finite set of generators:
public class GeneratedGroup<T> implements Group<T> {
private Set<T> generators;
private Set<T> elements;
private T identity;
private BiFunction<T, T, T> operation;
public GeneratedGroup(Set<T> generators, T identity, BiFunction<T, T, T> operation) {
this.generators = generators;
this.identity = identity;
this.operation = operation;
}
@Override
public Set<T> getElements() {
if (elements==null) {
elements = new HashSet<>(generators);
elements.add(getIdentity());
int size = 0;
while (size<elements.size()) {
size = elements.size();
Set<T> generated = new HashSet<>();
for (T t : elements) {
for (T g : generators) {
generated.add(multiply(t, g));
}
}
elements.addAll(generated);
}
}
return elements;
}
...
}
Again, simple implementation details are left out.
The thing worth mentioning here is the
getElements function, implemented lazily.
On first invocation, it will generate the set of elements based on the identity element and the set of generators using a fixed point approach:
- We start with the set of elements consisting of the identity element only.
- We then keep applying all generators to all elements of this set, and adding these as new elements, until the set no longer grows in size.
The Pauli Group
We now have sufficient building blocks to implement a first version of the Pauli group, with matrices as elements, using generators. We will be using the matrices introduced in Generating the Pauli Group.
We will be borrowing the matrix implementation of our previous post about quantum computing, Hadamard and Friends. And we have an alphabet of matrices ready:
public class Alphabet {
public static final Matrix I = MatrixUtils.identity(2);
public static final Matrix X = new Matrix("X", new Double[][] { { 0d, 1d }, { 1d, 0d } });
public static final Matrix Y = new Matrix("Y", new Double[][] { { 0d, -1d }, { 1d, 0d } }).cmul(Complex.I).setName("Y");
public static final Matrix Z = new Matrix("Z", new Double[][] { { 1d, 0d }, { 0d, -1d } });
...
}
Multi-dimensional complex array constants are cumbersome to write, and the
Matrix implemention is immutable.
Therefore, we have to rename the matrix \(Y\) after multiplication with the complex number \(i\).
The Pauli group can now easily be defined as:
public class GroupUtils {
public static Group<Matrix> getPauliGroup() {
Set<Matrix> generators = new HashSet<>(Arrays.asList(Alphabet.X, Alphabet.Y, Alphabet.Z));
return new GeneratedGroup<Matrix>(generators, Alphabet.I, (a, b) -> a.vmul(b));
}
...
}
Cyclic Groups
For the alternative implementation of the pauli group, we first need a cyclic group of order four. We cannot define this group as the quotient \(\mathbb{Z}/4\mathbb{Z}\), as we can only handle finite groups. We will therefore explicitly define modulo numbers and once more use a generated group.
public class Modulo {
private int value;
private int modulo;
public Modulo(int value, int mod) {
this.value = value%mod;
this.modulo = mod;
}
public Modulo add(Modulo m) {
return new Modulo(value+m.getValue(), modulo);
}
...
}
Completing the implementation is straightforward. We added the implementation of the group operation
add, just in case.
The cyclic group of order four can now be easily defined as:
public class GroupUtils {
public static Group<Modulo> getCyclicGroup(int size) {
HashSet<Modulo> generators = new HashSet<>(Arrays.asList(new Modulo(1, size)));
return new GeneratedGroup<Modulo>(generators, new Modulo(0, size), (a, b) -> a.add(b));
}
...
}
The Dihedral Group of Order Eight
The dihedral group of order eight can equally be defined as a generated group, using the matrices introduced in The Dihedral Group of a Square. Therefore, this section is very similar to the one where we introduced the matrix representation of The Pauli Group.
First we need the matrix definitions:
public class Alphabet {
public static final Matrix R = new Matrix("R", new Double[][] { { 0d, -1d }, { 1d, 0d } });
public static final Matrix M = new Matrix("M", new Double[][] { { 1d, 0d }, { 0d, -1d } });
...
}
Then we are ready to create the group:
public class GroupUtils {
public Group<Modulo> getDihedral8Group() {
Set<Matrix> generators = new HashSet<>(Arrays.asList(Alphabet.R, Alphabet.M));
return new GeneratedGroup<Matrix>(generators, Alphabet.I, (a, b) -> a.vmul(b));
}
...
}
The Center of a Group
Comes the time we need to compute the center of a group:
public class GroupUtils {
public static <T> Group<T> getCenter(Group<T> group) {
Set<T> center = group.getElements().stream()
.filter(z -> group.getElements().stream()
.filter(g -> !group.multiply(z, g).equals(group.multiply(g, z))).count()==0l)
.collect(Collectors.toSet());
return new EnumeratedGroup<T>(center, group.getIdentity(), group::multiply);
}
...
}
We provide a stream style implementation, that filters all elements of the group (the outer filter) that commute with all elements of the group (the inner filter) to determine the elements of the center. We then use that set to create an enumerated group with the same identity element and the same group operation.
The Direct Product
By now, the exercise risks becoming just more of the same thing. We can implement the direct product of two groups as the Cartesian product of the elements in the group with the pairwise group operations.
public class ProductGroup<T, S> implements Group<Pair<T, S>> {
private Group<T> tgroup;
private Group<S> sgroup;
private Set<Pair<T, S>> elements;
public ProductGroup(Group<T> tgroup, Group<S> sgroup) {
this.tgroup = tgroup;
this.sgroup = sgroup;
}
@Override
public Set<Pair<T, S>> getElements() {
if (elements==null) {
elements = new HashSet<>();
for (T t : tgroup.getElements()) {
for (S s : sgroup.getElements()) {
elements.add(new Pair<>(t, s));
}
}
}
return elements;
}
@Override
public Pair<T, S> getIdentity() {
return new Pair<>(tgroup.getIdentity(), sgroup.getIdentity());
}
@Override
public Pair<T, S> multiply(Pair<T, S> a, Pair<T, S> b) {
return new Pair<>(tgroup.multiply(a.getT(), b.getT()), sgroup.multiply(a.getS(), b.getS()));
}
...
}
We us a
Pair to combine two elements, one of each group.
You can use any implementation you can find, or write your own.
Just make sure to implement equals and hashcode in a proper way.
Again we have a lazy implementation of the getElements method that calculates the Cartesian product of the elements of the two groups as a set of pairs. The identity element is the pair of the identity elements of both groups. The operation is the pairwise multiplication of the elements of both groups.
Quotient Groups
The implementation of a quotient group however is a bit trickier:
public class QuotientGroup<T> implements Group<T> {
private Group<T> group;
private Set<T> subgroup;
private Set<T> elements;
private Map<T, Set<T>> representation;
public QuotientGroup(Group<T> group, Set<T> subgroup) {
this.group = group;
this.subgroup = subgroup;
}
@Override
public Set<T> getElements() {
if (elements==null) {
elements = new HashSet<>();
representation = new HashMap<>();
Set<Set<T>> cosets = new HashSet<>();
for (T e : group.getElements()) {
Set<T> coset = GroupUtils.multiply(group, subgroup, e);
if (!cosets.contains(coset)) {
elements.add(e);
representation.put(e, coset);
cosets.add(coset);
}
}
}
return elements;
}
@Override
public T getIdentity() {
return group.getIdentity();
}
private T normalize(T t) {
T n = GroupUtils.findElement(representation, t);
if (n!=null) {
return n;
}
return t;
}
@Override
public T multiply(T a, T b) {
return normalize(group.multiply(a, b));
}
...
}
We start with a group and a subgroup, the latter represented as a set of elements only. In addition to that, the impementation will keep track of the set of elements, as most of the
Group implementations.
However, as we will represent each coset by a unique representative of the coset, we need to keep track of which element represents which coset.
This is done using the representation, a mapping of represtatives to cosets.
As before, the elements are determined lazily. To determine the set of elements, we scan the elements of the larger group and determine the coset of the smaller group for each element. Is this is a new coset, we use the element as a representative for that coset, and update the representation map. If we already have the coset, we replace the element by its representation.
The
getElements function uses a utility function GroupUtils.multiply for this purpose, that determines the coset of an element of the group:
public class GroupUtils {
public static <T> Set<T> multiply(Group<T> group, Set<T> elements, T element) {
return elements.stream().map(e -> group.multiply(e, element)).collect(Collectors.toSet());
}
...
}
The
QuotientGroup implementation has a private member function normalize that does the same thing, replacing an element by its unique representative, that we use after every calculation.
For now, that is only in the multiply function.
It uses another utility function GroupUtils.findElement, that finds the coset in the representation map that contains a newly created element, and returns the representation of that coset:
public class GroupUtils {
public static <T> T findElement(Map<T, Set<T>> map, T t) {
for (T r : map.keySet()) {
if (map.get(r).contains(t)) {
return r;
}
}
return null;
}
...
}
The Central Product
We now have sufficient building blocks to implement the second version of the Pauli group, as the central product of the cyclic group of order four and the dihedral group of a square.
public class GroupUtils {
public static <T> Group<Pair<Modulo, Matrix>> getCentralProductPauliGroup() {
Group<Modulo> cyclic4 = getCyclicGroup(4);
Group<Matrix> dihedral8 = getDihedral8Group();
Group<Pair<Modulo, Matrix>> product = new ProductGroup<>(cyclic4, dihedral8);
Set<Pair<Modulo, Matrix>> subgroup = getCentralProductPauliSubGroup();
return new QuotientGroup<>(product, subgroup);
}
public static <T> Set<Pair<Modulo, Matrix>> getCentralProductPauliSubGroup() {
Set<Pair<Modulo, Matrix>> subgroup = new HashSet<>();
subgroup.add(new Pair<>(new Modulo(0, 4), Alphabet.I));
subgroup.add(new Pair<>(new Modulo(2, 4), r.vmul(r)));
return subgroup;
}
...
}
Note that we explicitly construct the subgroup of the direct product isomorphic to the maximum common subgroups of the centers of both factor groups of the direct product. Let's say we leave the generic implementation of that step as an exercise.
Finding an Isomorphism
Verifying whether a mapping between groups is an isomorphism is easy. Assume we represent the isomorphism as a mapping of elements from one group to the other:
public class GroupUtils {
public static <T, S> boolean isIsomorphism(Group<T> tgroup, Group<S> sgroup, Map<T, S> map) {
if (tgroup.getElements().size()!=sgroup.getElements().size()) {
return false;
}
for (T a : tgroup.getElements()) {
for (T b : tgroup.getElements()) {
if (!map.get(tgroup.multiply(a, b)).equals(sgroup.multiply(map.get(a), map.get(b)))) {
return false;
}
}
}
return true;
}
...
}
If the number of elements in both groups is different, the groups cannot possibly be isomorphic. Otherwise, we just check any combination of two elements of the first group, and verify whether the product of the images of the elements equals the image of the product. Any mismatch will refute the isomorphic character of the mapping.
Finding an isomorphism between two groups is trickier. Suppose we have generators for both groups, then we can gradually construct the isomorphism, and check for inconsistencies along the way:
public class GroupUtils {
public static <T, S> Map<T, S> getIsomorphism(Group<T> tgroup, Group<S> sgroup, List<T> tgenerators, List<S> sgenerators) {
if (tgenerators.size()!=sgenerators.size()) {
return null;
}
Map<T, S> isomorphism = new HashMap<>();
isomorphism.put(tgroup.getIdentity(), sgroup.getIdentity());
for (int i=0; i<tgenerators.size(); ++i) {
isomorphism.put(tgenerators.get(i), sgenerators.get(i));
}
int size = 0;
while (isomorphism.size()>size) {
size = isomorphism.size();
Map<T, S> mapping = new HashMap<>();
for (T t1 : isomorphism.keySet()) {
for (T t2 : isomorphism.keySet()) {
T tproduct = tgroup.multiply(t1, t2);
S sproduct = sgroup.multiply(isomorphism.get(t1), isomorphism.get(t2));
S expected = isomorphism.get(tproduct);
if (expected==null) {
expected = mapping.get(tproduct);
}
if (expected==null) {
mapping.put(tproduct, sproduct);
} else if (!sproduct.equals(expected)) {
return null;
}
}
}
isomorphism.putAll(mapping);
}
return isomorphism;
}
...
}
In what follows we will refer to the first group as the domain of the isomorphism and to the second group as the image of the isomorphism.
We assume that the list of generators that are provided for both groups already reflect the isomorphism. Therefore, they should be of equals size.
Then we initialize the isomorphism with the generators. We then extend the isomorphism by trying all combinations of elements in the domain, and calculating the products of their images and the image of their product. If the product is not yet present in the domain of the isomorphism, we add a mapping. If the product is present already, its image in the isomorphism should be equals to what we just calculated.
Because we cannot iterate over a collection while it is being modified, we accumulate new mappings in a separate data structure. We then merge all new mappings into the isomorphism after all combination of elements in the domain have been processed.
We repeat this process until the isomorphism no longer grows in size, effectively finding a fixed point for the process. Under the assumption that the initial elements provided are generators for the doamin and the image of the isomorphism, respectively, the fixed point will represent an isomorphism between both groups.
We realize this is all a bit messy, but we basically come to the same conclusion as Naftali Harris on this subject: finding an isomorphism between two groups is not a trivial task. However, using generators will reduce the complexity in a significant way.
Selecting Generators
The only step remaining to close the loop here, is finding the generators for the image. We will leave out the coding details, but give you the results.
We already have the generators for the domain, being \(X\), \(Y\) and \(Z\). Starting with all 16 elements of the image, we can limit ourselves to those that are a root of the identity element, as we know this condition holds for the generators of the domain. Excluding the identity itself, we find 7 elements that square to the identity:
[(0,M), (0,RR), (0,RM), (0,MR), (0,RRM), (1,R), (1,RRR)]
If we try each combination of three elements out of this set, no repetition, order matters, we get \(7!/3!=210\) possible combinations. Out of these, it turns out that \(48\) can be used to construct an isomorphism.
Knowing that the group structure is invariant under permutations of those three generators, and there are \(3!=6\) permutations of three elements, we get \(48/6=8\) combinations, ignoring order, that do the job. Here they are:
[ [(0,M), (0,RM), (1,R)], [(0,M), (0,RM), (1,RRR)], [(0,M), (0,MR), (1,R)], [(0,M), (0,MR), (1,RRR)], [(0,RM), (0,RRM), (1,R)], [(0,RM), (0,RRM), (1,RRR)], [(0,MR), (0,RRM), (1,R)], [(0,MR), (0,RRM), (1,RRR)] ]
Conclusions
Wrapping the standard Java
Set interface and its implementations with some additional characteristics provides an easy way to implement finite groups and play around with them.
As can be expected however, one quickly gets into the realms of NP-complete problems.
For the Pauli group on a single qubit, the limited quantitative complexity helped us to gain some insights.